インカムアプローチ・ロイヤルティ免除法・DCF法についての備忘録①

更新日 ： 2018.09.12

先週、日本弁理士会の知財価値評価事業本部の研修に参加しました。ロイヤルティ免除法やフリー・キャッシュ・フローの簡単な計算演習もあり、知識の再確認をすることができました。

知的財産価値評価ではロイヤルティ免除法やDCF法という用語が出てきます。このコラムでもときどきこれらの用語が登場しますが、特に体系的な説明はしてきませんでした。詳細な説明は他の専門書に譲るとして、今日はこれらの用語について再確認したことを備忘録的に書き留めておきたいと思います。

ロイヤルティ免除法もDCF法も、知的財産のような無形資産の評価法の一つであるインカム・アプローチを採用する場合に登場する言葉です。

インカムアプローチとは

インカム・アプローチというのは、「将来のキャッシュ・フローの割引現在価値で示す評価アプローチであり、将来生み出されるキャッシュ・フローの割引現在価値のうち当該無形資産に帰属する価値をもって無形資産の価値とする」ものです（日本公認会計士協会経営研究調査会報告 第57号 「無形資産の評価実務―M&A会計における評価とPPA業務－」（平成28年6月14日、第33頁）。この説明だけでは難しいので、特許権のロイヤルティ免除法を例にとって、もう少し簡単に説明してみたいと思います。

ロイヤルティ免除法とは

インカム・アプローチの手法の一つに、「ロイヤルティ免除法」というものがあります。これは「免除ロイヤルティ」をキャッシュ・フローとして考えるインカム・アプローチです。「免除ロイヤルティ」とは、「もし自分がその特許権を持っていなかったと仮定したら特許権者である他者にロイヤルティを支払っていたであろうが、実際は自分自身が特許権者なので他者への支払いを免れたことになる、そのロイヤルティ」のことです。「免除」という言葉があるので、特許権者側から見た表現になっています。これではちょっとわかりづらいので、ライセンスを受ける実施権者（ライセンシー）の立場から表現すれば、「当該特許権を利用することによる将来予測売上高にロイヤルティレートを乗じて求めた予想支払ロイヤルティ額」ということになります（上記報告、第62頁）。

上記のインカム・アプローチの定義で言えば『将来生み出されるキャッシュ・フローの割引現在価値のうち当該無形資産に帰属する』部分が免除ロイヤルティに該当します。その割引現在価値をもって特許権の価値とするのです。

より具体的に説明すると、例えば1年後から5年後までの売上予想額の各々にロイヤルティ料率をかけて、1年後から5年後までの各年度のロイヤルティ（免除ロイヤルティ）の額を求めたとします。これがインカム・アプローチでいうところの「将来キャッシュ・フロー」となります。この免除ロイヤルティの1年目から5年目までの合計額が、大ざっぱに言えば、その特許権の価値を計算する基礎になると考えるのです。しかし、そのまま合計するわけにはいきません。求めた各年度の免除ロイヤルティを合計する前に、各々の金額を現在価値に割り引く操作が必要になります。

DCF法とは

この現在価値に割り引く計算手法をDCF法と言います。DCFとはDiscounted Cash Flowの略です。将来のキャッシュフロー(Cash Flow)を現在価値に割り引く(Discount)ことを表しています。今日のコラムではDCF法を、各年度のキャッシュフローを現在価値に割り引く計算手法のことを指す用語として用いていますが、DCF法を用いるインカム・アプローチの手法を「DCF法」とまとめて定義することもあります。この定義によれば、ロイヤルティ免除法も「DCF法」の一手法であるという言い方もできます。また、インカム・アプローチの他の手法である寄与率法や利益分割法のことを「DCF法」という場合もあります。混乱を招くので、今日のコラムでは将来のキャッシュフロー(Cash Flow)を現在価値に割り引く計算手法だと思っていただければ十分です。

現在価値に割り引くとは

さて、そもそも「現在価値に割り引く」とはどういうことでしょうか？会計の専門ではない筆者の言葉で大ざっぱに言わせてもらえば、例えば、1年もの、2年もの、3年もの、4年もの、5年ものと各年度ごとに満期が来る５つの複利の定期預金があったとします。その将来の元金と利子の合計額、すなわち元利合計FV(Future Value)だけが先にわかっているという状況を考えてください。この場合、例えば3年後の元利合計FV3が先にわかっていたとして、これから元金を求めることを考えます。

[元利合計FV3] = [元金] x (1+r)³

ですから、元金はその逆算として、1/(1+r)³ を掛ければよいので、

[元金] = [元利合計FV3] x (1/(1+r)³)

ですね。各年度の元利合計FVi（i＝1～5）について、同様に金利ｒ（一定）として複利計算の逆算（つまり1/(1+r)ⁿを乗じる）を行なえば、５つの定期預金の割引現在価値、すなわち元金Pi（i＝1～5）を求めることができます。それらを合計したものが、それら５つの定期預金の現在価値PV(Present Value)であるというイメージです。

ただし、DCF法ではｒは金利ではなく割引率という言い方を用います。金利は将来に向けて複利で元金が増えていくイメージですが、割引率は元利合計から逆算して元金に相当する金額にまで減じるイメージから命名されているので、割引率という（減っていくイメージの）表現になっているようです。しかし割引率は、別の言い方をすれば、無形資産に対して投資家や債権者が収益を期待する「期待収益率」であるとも言えます。期待収益率という語感からすれば、金利と同様に増えていくイメージになります。結局、ｒを現在から将来に向けて考えるか（期待収益率）、将来から現在に向けて考えるか（割引率）で表現が変わるということです。実際には、割引率（期待収益率）は金利よりも大きい値となります。

さて、1年後から5年後までの各年度のキャッシュフロー（免除ロイヤルティ）を、各年度ごとに割引率ｒを用いて逆算します。各年度ごとにキャッシュフローを1/(1+r)ⁿ倍すれば割引現在価値となります。この1/(1+r)ⁿを割引係数とか、割引現価係数と呼ぶことがあります。これらを１～５年分合計した額がDCF法を用いたインカム・アプローチでの価値評価となります。

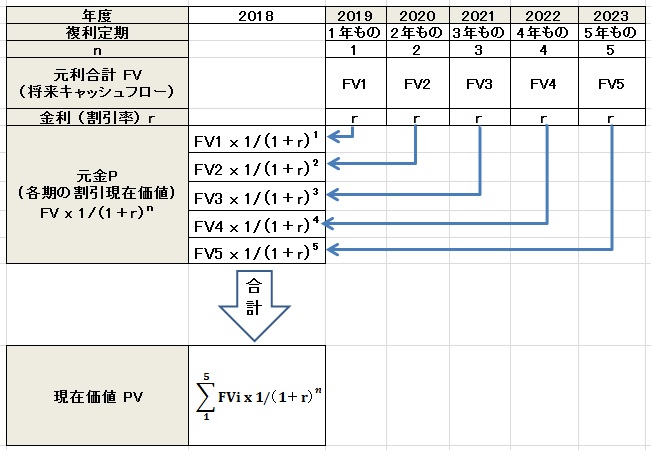
下図は元利合計と将来キャッシュフロー、金利と割引率、元金と各期割引割引現在価値とを対比させて「現在価値に割り引く」を説明するものです。

 

インカム・アプローチは評価対象である知的財産権の将来の経済的価値を把握したうえで現在価値に割り戻している点で合理的であると考えられ、会計の世界でも受け入れられやすいとされています。そしてロイヤルティ免除法は、知的財産権の将来のキャッシューフローを算定する際に基本的にロイヤルティ料率を考えれば済むという点で比較的簡単な手法です。また例えば特許権であれば、発明技術の優位性や特許性の強弱などに立ち入ってロイヤルティ料率を決定したり、商標権であれば標章の自他商品識別力やブランド力などに立ち入ってロイヤルティ料率を決定したりするので、弁理士による価値評価に向いているといえます。特許発明の技術的考察や登録商標の機能を考察せずに、財務諸表だけから無形資産の価値を評価する手法に比べると、説得性も出てくるのです。